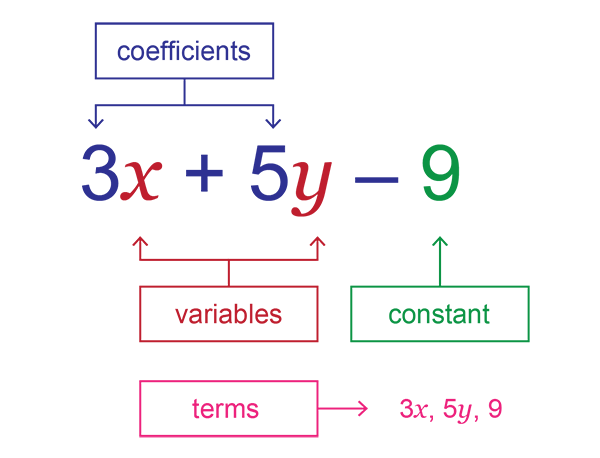
What are ‘Like Terms’ in a Math Expression?

You must know about the basics of algebra before understanding the concept of like terms in mathematics. Algebra, along with number theory, geometry, and analysis, is one of the broad topics of mathematics. Algebra, in its broadest sense, is the study of mathematical symbols and the rules for manipulating them. It is a thread that runs through virtually all of mathematics. It covers everything from solving simple equations to studying abstractions like groups, rings, and fields. Elementary algebra refers to the more fundamental aspects of algebra, whereas abstract algebra or contemporary algebra refers to the more abstract aspects. Elementary algebra is often regarded as a prerequisite for any study of mathematics, science, or engineering, as well as medical and economic applications.

Algebra began with arithmetic-style computations, with letters standing in for numbers. This allows for proof of characteristics that are true regardless of the numbers used. For instance, consider the quadratic equation,

ax²+bx+c=0

Here, a, b, and c can be any numbers, and the quadratic formula can be utilized to determine the values of the unknown quantity x that fulfill the equation fast and simply. To put it another way, to find all of the equation’s solutions.

The study of algebra has traditionally, and still does today, begin with the solution of problems like the quadratic equation above. After that, more general issues are examined, such as “does an equation have a solution?” “How many solutions does an equation have?” and “what can be stated about the nature of the solutions?” These inquiries led to the expansion of algebra to include non-numerical objects like permutations, matrices, vectors, and polynomials. These non-numerical objects’ structural characteristics were subsequently abstracted into algebraic structures like rings, groups, and fields.

Mathematics was split into only two subfields until the 16th century: arithmetic and geometry. Even if certain methods established much earlier are today called algebra, the development of algebra and, shortly after, infinitesimal calculus as subfields of mathematics dates only from the 16th or 17th century. Many new disciplines of mathematics emerged in the second half of the nineteenth century, the majority of which utilized both arithmetic and geometry, and virtually all of which employed algebra.

What do you mean by “like terms”?

Like words in algebra are those that contain the same variable raised to the same power. Only the numerical coefficients can alter in algebraic terms. We can combine like terms to simplify algebraic equations, making it much easier to find the result of the expression.

5x + 9x is an algebraic expression with like terms, for example. We may use similar words to simplify this algebraic statement. As a result, the provided statement has been simplified 14 times. You can execute all arithmetic operations on similar terms in the same way.

What do you mean by “unlike terms”?

Unlike terms are algebraic expressions that do not have the same literal coefficients and cannot be raised to the same power.

4x + 9y, for example, is an algebraic expression with unlike terms. Because it contains two distinct variables, x and y, and they are not raised to the same power.

Here are some tips for you to learn algebra easily

• Carefully read the problem instructions. When you have one or more math problems, you must carefully study the directions. Look for important terms like “solve,” “simplify,” “factor,” or “reduce” in the instructions. These are some of the most typical commands (although there are others that you will learn). Many individuals encounter issues when they try to “fix” a problem when all they need to do is “simplify.”
• Perform operations. You should find the key phrases in the problem instructions and then conduct the procedures.
• The terms “expression” and “equation” are not interchangeable. The distinction between an “expression” and an “equation” is critical in algebra. Any combination of numbers and variables gathered together is referred to as an expression. XY, 56xyz, and XYZ are two examples of expressions. An expression may only be factored or simplified. An = symbol appears in an equation, on the other hand. Equations can be simplified or factored in, but they can also be solved for a final result. It’s critical to seek the distinction.
• Learn how to use PEMDAS. The actions you perform in algebra must be in a logical order, which is known as the “order of operations.” The mnemonic device “PEMDAS” is frequently used to simplify this. PEMDAS letters will show you which operations to do in which sequence. The letters of PEMDAS stand for: Parentheses, Exponents., Multiplication, Division, Addition, Subtraction.
• You must brush up on your concepts of addition, subtraction, multiplication, and division from the previous class to understand or solve the problem of algebra. Make sure that your basics are strong. This will help you to learn algebra quickly.

Learn more from Algebraic Expressions

We hope the above information is helpful for you.